- Римана интеграл
- Содержание
- Неформальное геометрическое описание
- Определения
- Через интегральные суммы
- Через суммы Дарбу
- Свойства
- История
- См. также
- Ссылки
- Смотреть что такое «Римана интеграл» в других словарях:
- Определенный интеграл Римана, Дарбу, Ньютона-Лейбница, виды интегрируемых функций
- Определенный интеграл Римана
- Определенный интеграл Дарбу
- Определенный интеграл Ньютона-Лейбница
- Необходимое условие интегрируемости функции на отрезке, виды интегрируемых функций
- Итоги
Римана интеграл
Интегра́л Ри́мана — одно из важнейших понятий математического анализа. Введён Бернхардом Риманом в 1854 году, и является одной из первых формализаций понятия интеграла.
Содержание
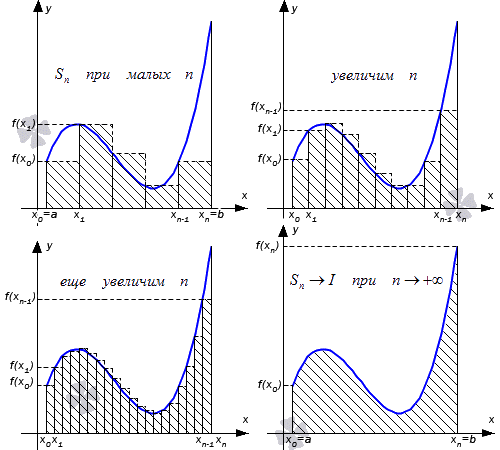
Неформальное геометрическое описание
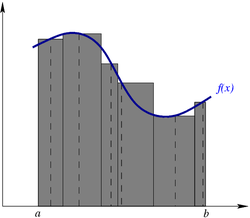
Риман формализовал понятие интеграла, разработанное Ньютоном и Лейбницем, как площади подграфика (фигуры, заключенной между графиком функции и осью абсцисс). Для этого он рассмотрел фигуры, состоящие из нескольких вертикальных прямоугольников и получающиеся при разбиении отрезка (см. рисунок). Если при «размельчении» разбиения существует предел, к которому сходятся площади таких фигур (интегральные суммы), этот предел называется интегралом Римана функции на отрезке.
Определения
Через интегральные суммы
Рассмотрим разбиение отрезка 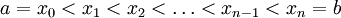

Отметим на каждом отрезке разбиения по точке 

Если при стремлении диаметра разбиения к нулю интегральные суммы стремятся к одному и тому же числу, независимо от выбора 
В этом случае, сама функция f называется интегрируемой (по Риману) на [a,b] ; в противном случае f является неинтегрируемой (по Риману) на отрезке [a,b] .
Через суммы Дарбу
Пусть на отрезке [a,b] определена вещественнозначная функция f . Рассмотрим произвольное разбиение отрезка 
Верхней суммой Дарбу Δ называется число
Соответственно, нижней суммой Дарбу для Δ называется
Функция называется интегрируемой по Риману, если существует вещественное число
В этом случае, по определению
Свойства
- Если функция F является первообразной функции f , то интеграл функции f на отрезке [a,b] может быть вычислен по формуле Ньютона-Лейбница: он равен F(b) − F(a) .
- Непрерывная на отрезке функция интегрируема по Риману. Разрывные функции могут быть интегрируемы, но могут и не быть; примером функции, не интегрируемой по Риману, является всюду разрывная функция Дирихле.
- Ограничение: Если функция f интегрируема на отрезке [a,b] , то она интегрируема и на меньшем отрезке [a1,b1] , где
.
- Если функция интегрируема на отрезке [a,b] и на отрезке [b,c] , то она интегрируема и на отрезке [a,c] , и
.
- Линейность: Если функции f и g интегрируемы, и
, то функция αf + βg тоже интегрируема, и
- Предел: Если интегрируемые функции fiравномерно сходятся на отрезке [a,b] к функции f , то f интегрируема, и
История
Такое определение интеграла дано Коши [1] , но применялось только для непрерывных функций.
Риман в 1854 году [2] , дал это же определение без предположения непрерывности.
См. также
Ссылки
- Таблицы неопределенных и определенных интегралов — EqWorld: Мир математических уравнений.
- ↑ Cauchy A. L., Sur la mécanique céleste et sur un nouveau calcul appelé calcul des limites, Turin 1831
- ↑ Riemann В., «Göttinger Akad. Abhandl.», 1868, Bd 13
Wikimedia Foundation . 2010 .
Смотреть что такое «Римана интеграл» в других словарях:
РИМАНА ИНТЕГРАЛ — обобщение понятия Коши интеграла на нек рый класс разрывных функций, введенное Б. Риманом (В. Riemann, 1853). Пусть функция f (х)задана на отрезке [ а, b]и . Сумму вида (1) где , наз. и н т е г р а л ь н о й с у м м о й, отвечающей данному… … Математическая энциклопедия
Римана интеграл — обычный определённый Интеграл. Само определение Р. и. по существу было дано О. Коши (1823), который, однако, применял его к непрерывным функциям. Б. Риман впервые указал (1853, опубликовано в 1867) необходимое и достаточное условие… … Большая советская энциклопедия
Интеграл Даниэля — Одна из основных трудностей в использовании традиционного интеграла Лебега состоит в том, что его применение требует предварительной разработки подходящей теории меры. Существует другой подход, изложенный Даниэлем (Daniell) в 1918 году в его… … Википедия
ИНТЕГРАЛ — одно из центральных понятий математич. анализа и всей математики, возникновение к рого связано с двумя задачами: о восстановлении функции по ее производной (напр., с задачей об отыскании закона движения материальной точки вдоль прямой по… … Математическая энциклопедия
Интеграл Даниеля — Одна из основных трудностей в использовании традиционного интеграла Лебега состоит в том, что его применение требует предварительной разработки подходящей теории меры. Существует другой подход, изложенный Даниелем (англ.) в 1918 году в его… … Википедия
Интеграл Курцвейля — Интеграл Курцвейля Хенстока обобщение интеграла Римана, позволяет полностью решить задачу о восстановлении дифференцируемой функции по её производной. Ни интеграл Римана (в том числе и несобственный), ни интеграл Лебега не дают… … Википедия
Интеграл Лебега — Стилтьеса — Интеграл Лебега это обобщение интеграла Римана на более широкий класс функций. Все функции, определённые на конечном отрезке числовой прямой и интегрируемые по Риману, являются также интегрируемыми по Лебегу, причём в этом случае оба интеграла… … Википедия
Интеграл Римана — Стилтьеса — Интеграл Римана Стилтьеса обобщение определённого интеграла, предложенное в 1894 году Стилтьесом. Вместо предела обычных интегральных сумм рассматривается предел сумм где интегрирующая функция j(x) есть функция с ограниченным… … Википедия
Интеграл (значения) — Интеграл (см. также Первообразная, Численное интегрирование, Интегрирование по частям) математический оператор: Определённый интеграл Неопределённый интеграл различные определения интегралов: Интеграл расширение понятия суммы Интеграл Ито… … Википедия
Интеграл Римана — Интеграл Римана Стилтьеса обобщение определённого интеграла, предложенное в 1894 году Стилтьесом. Вместо предела обычных интегральных сумм рассматривается предел сумм где интегрирующая функция есть функция с ограниченным изменением… … Википедия
Источник
Определенный интеграл Римана, Дарбу, Ньютона-Лейбница, виды интегрируемых функций
Определение интеграла было дано еще в школе при вычислении площади криволинейной трапеции. Была рассмотрена непрерывная неотрицательная функция y = f ( x ) на отрезке [ a ; b ] , тогда сам отрезок развивался на n равных частей точками a = x 0 x 1 x 2 . . . x n — 1 x n = b . Отсюда получали, что площадь криволинейной трапеции была представлена в виде площадей элементарных треугольников
S n = f ( x 0 ) · ( x 1 — x 0 ) + f ( x 1 ) · ( x 2 — x 1 ) + . . . + f ( x n — 1 ) · x n — x n — 1 = = f ( x 0 ) · b — a n + f ( x 1 ) · b — a n + . . . + f ( x n — 1 ) · b — a n = = b — a n · f ( x 0 ) + f ( x 1 ) + . . . + f ( x n — 1 )
Значение данного выражения стремилось к числу I при бесконечном увеличении количества точек разбиения отрезка [ a ; b ] .
После обобщения выражения и определения получили, что любая непрерывная функция y = f ( x ) с числом I имеет отрезок, который и получил название определенного интеграла.
Его геометрическое понятие было показано в школе в 11 классе. Рассмотрим рисунок, приведенный ниже. Имеем изображение определенного интеграла.
В данной статье будет показано определения определенного интеграла, которые были заданы Риманом и Дарбу, Ньютоном-Лейбницом. Подробно будет показано условие интегрируемости функции на заданном определенном отрезке с перечислением интегрируемых функций.
Определенный интеграл Римана
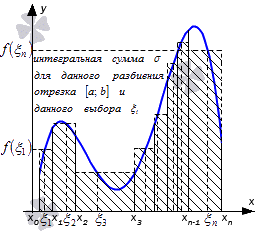
Рассмотрим функцию y = f ( x ), которая определяется на заданном отрезке [ a ; b ] . Необходимо разбить даны отрезок на n количество частей x i — 1 ; x i , i = 1 , 2 , . . . , n точками a = x 0 x 1 x 2 . . . x n — 1 x n = b . Примем обозначение λ = m a x i = 1 , 2 , . . . , n ( x i — x i — 1 ) , а сами точки x i , i = 1 , 2 , . . . , n — 1 необходимо выбрать таким образом, чтобы λ → 0 при n → + ∞ . В выбранном отрезке x i — 1 ; x i , i = 1 , 2 , . . . , n необходимо выбрать точку ζ i . При заданных условиях существует множество способов выбора точек x i , i = 1 , 2 , . . . , n — 1 и ζ i , i = 1 , 2 , . . . , n .
Интегральная сумма функции y = f ( x ) для разбиения отрезка [ a ; b ] с выбором точек ζ i , i = 1 , 2 , . . . , n является выражение вида:
σ = f ( ζ 1 ) · x 1 — x 0 + f ( ζ 2 ) · x 2 — x 1 + . . . + f ( ζ n ) · ( x n — x n — 1 ) = = ∑ i = 1 n f ( ζ i ) · ( x i — x i — 1 )
Рассмотрим рисунок, приведенный ниже.
Для того, чтобы разбить заданный отрезок [ a ; b ] и выбрать точки ζ i , i = 1 , 2 , . . . , n , получаем интегральную сумму. Иначе говоря, получаем множество интегральных сумм с различными вариациями выбора x i , i = 1 , 2 , . . . , n и ζ i , i = 1 , 2 , . . . , n .
Число I называют пределом интегральных сумм σ при λ → 0 , когда любое малое положительное эпсилон ε > 0 имеет место быть малым положительным, зависящим от эпсилон, причем δ ( ε ) > 0 , с λ δ , тогда при выборе точек ζ i , i = 1 , 2 , . . . , n неравенство σ — I ε считается справедливым.
Интегрируемой на отрезке [ a ; b ] функцией y = f ( x ) называют такую функцию, у которой имеется конечный предел ее интегральных сумм при λ → 0 . Данное значение предела называют определенным интегралом Римана.
За обозначение интеграла Римана принято брать выражение вида ∫ a b f ( x ) d x . Из определения получим, что определенный интеграл Римана записывается так: ∫ a b f ( x ) d x = lim λ → 0 σ .
Числа a и b называют нижним и верхним пределом интегрирования, а f ( x ) – подынтегральная функция, где x – переменная интегрирования.
Значение определенного интеграла Римана не зависит от переменной интегрирования , тогда получаем интеграл вида ∫ a b f ( x ) d x = ∫ a b f ( t ) d t = ∫ a b f ( u ) d u = ∫ a b f ( q ) d q .
Определенный интеграл Дарбу
Чтобы понять необходимо и достаточное условие существования определенного интеграла Дарбу, необходимо применить несколько определений.
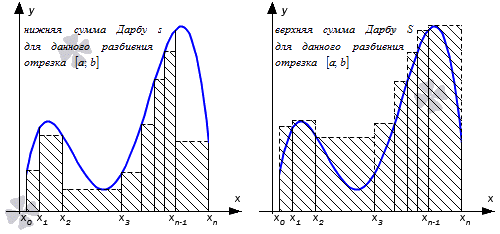
Возьмем на рассмотрение функцию y = f ( x ) , определенную на отрезке [ a ; b ] . Необходимо разбить заданный отрезок на n количество частей при помощи точек a = x 0 x 1 x 2 . . . x n — 1 x n b с условием λ → 0 при n → + ∞ . Тогда m i и M i являются нижней и верхней гранью множества значений заданной функции на i -ом отрезке i = 1 , 2 , . . . , n . Получаем, что для непрерывной и ограниченной функции m i = m i n x ∈ x i — 1 ; x i f ( x ) , M i = m a x x ∈ x i — 1 ; x i f ( x ) , i = 1 , 2 , . . . , n .
s = m 1 · ( x 1 — x 0 ) + m 2 · ( x 2 — x 1 ) + . . . + m n · ( x n — x n — 1 ) = = ∑ i = 1 n m i · ( x i — x i — 1 )
S = M 1 · ( x 1 — x 0 ) + M 2 · ( x 2 — x 1 ) + . . . + M n · ( x n — x n — 1 ) = = ∑ i = 1 n M i · ( x i — x i — 1 )
для разбиения отрезка [ a ; b ] называют нижней и верхней суммами Дарбу.
Рассмотрим рисунок, приведенный ниже.
Отсюда видно, для того, чтобы разбиение данного отрезка было фиксированным, необходимо использовать двойное неравенство s ≤ σ ≤ S , которое является справедливым. Иначе говоря, s и S считаются нижней и верхней гранями множества интегральных сумм.
Интегрируемость функции y = f ( x ) на отрезке [ a ; b ] должна иметь достаточное условие, которое дает предел разности верхней и нижней сумм Дарбу равным нулю при λ → 0 , тогда условие lim λ → 0 ( S — s ) = 0 выполняется. Это и есть необходимое и достаточное условие существования определенного интеграла Дарбу, который так и получил название определенный интеграл Дарбу. Его обозначение записывается в виде ∫ a b f ( x ) d x .
Определенный интеграл Ньютона-Лейбница
Рассмотрим подробно понятие определенного интеграла Ньютона-Лейбница.
Если функция вида y = f ( x ) имеет первообразную F ( x ) , определенную на отрезке [ a ; b ] , со значением первообразной в точке х = а равняется нулю, то есть F ( a ) = 0 . Определенный интеграл Ньютона-Лейбница — значение первообразной в точке интегрирования b , тогда получаем выражение вида ∫ a b f ( x ) d x = F ( b ) при F ( a ) = 0 .
Данное определение связано в формулой Ньютона-Лейбница ∫ a b f ( x ) d x = F ( b ) — F ( a ) . В ней F ( x ) является первообразной из множества, а определенный интеграл имеет первообразную, которая становится равной нулю при х = а .
Необходимое условие интегрируемости функции на отрезке, виды интегрируемых функций
Рассмотрим необходимое условие существования определенного интеграла функции на отрезке.
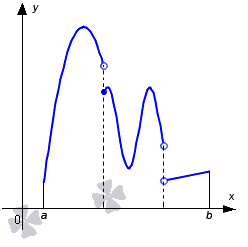
Когда функция вида y = f ( x ) интегрируема на отрезке [ a ; b ] , то имеется в виду, что она им ограничена. Условие считается необходимым, но не достаточным, так как функция ограничена отрезком, при этом она не всегда на нем интегрируема. Это условие применяют для проверки возможности интегрирования имеющейся функции на заданном отрезке. Иначе говоря, проверяется ее ограниченность.
Виды функций, для которых существует определенный интеграл:
- когда функция непрерывна на отрезке [ a ; b ] , значит интегрируема;
- когда функция ограничена на отрезке [ a ; b ] и непрерывна в точках, кроме конечного числа, тогда считается, что она интегрируема на отрезке [ a ; b ] .
Рассмотрим рисунок, приведенный ниже. На нем располагается пример интегрируемой функции.
Итоги
Задавание определенного интеграла Римана происходит через предел интегральных сумм, а интеграл Дарбу – предел разности верхних и нижних сумм Дарбу, в свою очередь интеграл Ньютона-Лейбница – при помощи значения первообразной.
Одновременное существование интеграла Римана и Ньютона-Лейбница, определенных на отрезке [ a ; b ] , возможно, при этом их значения будут равными. Для ограниченной функции существование определенного интеграла Дарбу и Римана невозможно.
Источник


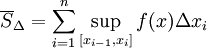
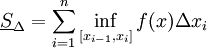

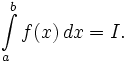
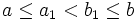 .
. .
.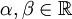 , то функция αf + βg тоже интегрируема, и
, то функция αf + βg тоже интегрируема, и